Разделы сайта

Методы нахождения передаточной функции

Передаточная функция следящей системы равна:

k(p)=(Tкзp+1)(Тупрp+1)[(Tэмp+1)Tяp+1]

где

A(p)=p(Ткзp+1)(Tупрp+1)[(Tэмp+1)Tяp+1]+kv=a5p+a4p+a3p+a2p+a1p+a0

характеристический многочлен разомкнутой системы

Т.к. а0=b0=kv мы можем переписать данную функцию в таком виде:

b0 Y(p)(p)= a5p+a4p+a3p+a2p+a1p+a0 X(p)

На основании данной функции запишем дифференциальное уравнение замкнутой системы. Оно имеет вид:

*dy/dt +a4*dy/dt +a3*dy/dt +a2*dy/dt +a1*d y/dt +a0*y=b0*x;

Для решения дифференциального уравнения численным методом его необходимо преобразовать к системе пяти уравнений 1го порядка, предварительно разделив все коэффициенты на старший коэффициент а5, получим:

dy/dt +a4¢*dy/dt +a3¢*dy/dt +a2¢*dy/dt +a1¢*dy/dt +a0¢*y=b0¢*x;

где ai¢ =ai/a5,(i=0,1,…,4); a0¢=b0¢=b0/a5;

Введём новую переменную z, тогда z1=y, z2=y¢, z3=y¢¢, z4=y¢¢¢, z5=y¢.

Преобразовав выражение представим систему в таком виде: dz1/dt=z2, dz2/dt=z3, dz3/dt=z4, dz4/dt=z5, dz5/dt=b0¢x-a0¢z1-a1¢z2-a2¢z3-a3¢z4-a4¢z5. В нашем случае используется метод Э2, начальные условия:

z1(0)=z2(0)=z3(0)=z4(0)=z5(0). В результате решения необходимо получить таблицу значений для функции z1(t)(при двух значениях: kvкрит/2 и kvкрит/4) h(t)=z1(t) - переходная функция - реакция системы на единичное ступенчатое воздействие, причем её значения должны затухать вокруг 1. Время t, при котором данная функция попадает в 5% коридор отклонения от значения 1 и не выходит из него называется tрег-время регулирования. По данным таблиц строим графики z1(t)=h(t). По найденным далее значениям t и t, соответствующих kv крит/2 и kv крит/4 вычисляем интегральные квадратичные оценки:

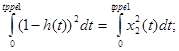
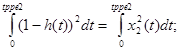
Определение значения интегралов производим по методу Симпсона.

Самое читаемое:

Метод частотной модуляции радиотехнического сигнала
За последнее время существенно повысился технический уровень электронной техники. Быстрое развитие требует создания все более точного и сложного автоматизированного технологического оборудования для изобретения более сложных и совершенных устройств с лучшими характеристиками и параметрами, меньшими габаритами. Для у ...