Разделы сайта

Численное интегрирование

Пусть требуется вычислить определенный интеграл

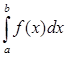(1.1)

где f(x) - непрерывная на отрезке [a; b] функция.

С геометрической точки зрения интеграл (1.1) при f(x) > 0 равен площади криволинейной трапеции, ограниченной кривой y = f(x), осью Ox и прямыми x = a, x = b (рис. 1.3). Другими словами, (1.1) равен площади заштрихованной фигуры на рис. 1.3

Рис. 1.3. Геометрический смысл определенного интеграла.

Вычислить определенный интеграл (1.1) можно с помощью аналитической формулы Ньютона-Лейбница 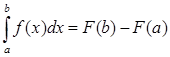(1.2):

(1.2)

где F(x) - первообразная функция для заданной функции f(x).

Однако во многих случаях не удается найти никакой аналитической формулы в виду невозможности определения F(x). В таких случаях приходится применять методы численного интегрирования. Задачи численного интегрирования приходится решать для функций, заданных таблично, функцией, интегралы от которых не берутся в элементарных функциях, и т.д.

Вместо функции, которую требуется проинтегрировать, проинтегрируем интерполяционный многочлен. Методы, основанные на замене подынтегральной функции интерполяционным многочленом, позволяют по параметрам многочлена оценить точность результата или же по заданной точности подобрать эти параметры.

Основной принцип построения всех приближенных формул численного интегрирования состоит в том, что интервал интегрирования разбивается на множество меньших отрезков, внутри которых подынтегральная кривая y = f(x) заменяется с некоторой степенью точности более простыми функциями, интегралы от которых можно вычислить. С геометрической точки зрения выполняется следующее: искомая площадь криволинейной трапеции приближенно заменяется суммой площадей элементарных геометрических фигур.

В процессе численного интегрирования необходимо вычислить приближенное значение интеграла и оценить погрешность. Погрешность уменьшается при увеличении n-количества разбиений отрезка . Однако при этом возрастает погрешность округления за счет суммирования значений интегралов, вычисленных на частичных отрезках.

Самое читаемое:

Мощный импульсный стабилизированный блок питания
Процесс в развитии науки и техники не стоит на месте. Большую роль в этом процессе играет технология, так как от правильно выбранной или разработанной технологии зависят и характеристики конкретного изделия и его стоимость. Необходимость проектирования сложных радиоэлектронных средств (РЭС) и требования к сокращению сроков их про ...