Разделы сайта
- Главная
- Исследования и анализ современных технологий
- IP-телефония
- Антенно-фидерные устройства
- Виртуальное построение рабочей локальной сети
- Влияние электромагнитного поля на подземную проволочную антенну
- Микрополосковая антенная решетка
- Система экологического мониторинга вредных газовых выбросов
- Организация процесса производства цифрового телевиденья
Вывод формулы Симпсона
Если для каждой пары отрезков 
построить многочлен второй степени, затем проинтегрировать его и воспользоваться свойством аддитивности интеграла, то получим формулу Симпсона.
Рассмотрим подынтегральную функцию 
на отрезке 
. Заменим эту подынтегральную функцию интерполяционным многочленом Лагранжа второй степени, совпадающим с в точках x0, x1 = x0 + h, x2 = x0 + 2h:
Проинтегрируем 
:
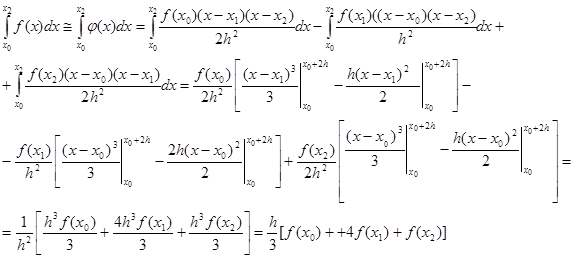
Формула:
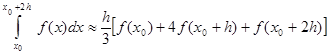
называется формулой Симпсона.
Полученное для интеграла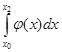 
значение совпадает с площадью криволинейной трапеции, ограниченной осью 
, прямыми 
, 
и параболой, проходящей через точки 
Оценим теперь погрешность интегрирования по формуле Симпсона. Будем считать, что у 
на отрезке 
существуют непрерывные производные f ʹ, f ʹʹ, f ʹʹʹ, f ʹʹʹʹ.
Составим разность:
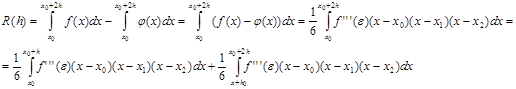
К каждому из этих двух интегралов уже можно применить теорему о среднем, поскольку 
непрерывна на и функция 
неотрицательна на первом интервале интегрирования и неположительна на втором ( то есть не меняет знака на каждом из этих интервалов). Поэтому:
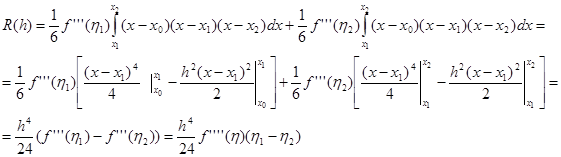
(воспользовались теоремой о среднем, поскольку - непрерывная функция; 
).
Дифференцируя 
дважды и применяя затем теорему о среднем, получим для другое выражение:
, где 
Из обеих оценок для следует, что формула Симпсона является точной для многочленов степени не выше третьей. Запишем формулу Симпсона в виде:
,
.
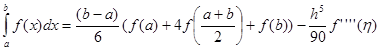Если отрезок 
интегрирования слишком велик, то его разбивают на 
равных частей (полагая 
), после чего к каждой паре соседних отрезков 
, 
, .,
применяют формулу Симпсона.
Формула Симпсона в общем виде:
Самое читаемое:
Изготовление цифрового прибора для контроля осанки и зрения при работе на персональном компьютере
Современную жизнь невозможно представить без электроники и ее важнейшей
отрасли - микроэлектроники. В любом месте - на работе и в быту - изделия из электроники
окружают человека. Она трудится повсюду - в сверхглубоких скважинах и в
подводных аппаратах - батискафах, в самолетах и космических кораблях, на
атомных электростанциях и рад ...