Разделы сайта

Распространение радиоволн в идеальном однородном диэлектрике

В такой среде e, m = Const, r = s = 0. Модель наиболее близка к распространению в нейтральной атмосфере. Для воздуха можно полагать, что магнитная проницаемость m = m0 = 4p×10-7 Гн / м, а диэлектрическая проницаемость e = e' e0 (e0 = 8,85×10-12 Ф / м, e¢ - относительная диэлектрическая проницаемость). Тогда система Максвелла принимает вид:

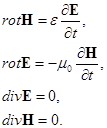(2.1)

Выведем уравнение, описывающее распространение радиоволн в такой среде. Применим к двум первым уравнениям (2.1) операцию rot:

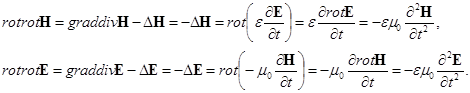
Получаем два дифференциальных уравнения второго порядка:

(2.2)

Будем полагать, что ток в излучающей антенне меняется по гармоническому закону, т. е. E, H ~ Cos wt (w - круговая частота), или в комплексной форме . Из представления напряжённости электрического поля E(r,t) = E(r)×eiwt следует, что , аналогичное соотношение получается и для H. Подстановка в (2.2) даёт

(2.3)

где введено обозначение .

Из электродинамики известно, что физически корректным и математически точным решением волнового уравнения вида (2.2) является распространяющаяся от источника сферическая волна, амплитуда которой (r - расстояние от излучателя). При решении многих задач распространения рассматриваются плоские радиоволны, которые определяются следующим образом: электромагнитная волна называется плоской, если вектор напряженности электрического (магнитного) поля имеет одну и ту же величину во всех точках любой плоскости, перпендикулярной направлению распространения волны. Такая плоскость, следовательно, является и поверхностью равных фаз.

Пусть плоская радиоволна распространяется вдоль оси Ox, т. е. E = E(x,t), H = H(x,t). После подстановки этих представлений в (2.3) и сокращения на временной множитель eiwt получим

(2.4)

Нетрудно проверить, что решения уравнений (2.4) для волны, распространяющейся в положительном направлении Ox, имеют вид

E(x) = Em×e-ikx, H(x) = Hm×e-ikx (2.5)

где Em и Hm - амплитуды полей. Таким образом, решения уравнений (2.3) для заданных условий имеют вид:

(2.6)

Из (2.6) следует, в частности, что поля E и H в распространяющейся волне синфазны.

Освободиться от специального выбора системы координат можно, используя волновой вектор k = kn (n - единичный вектор, направленный по пути распространения радиоволны). Если r - радиус-вектор точки на поверхности фронта волны (рис. 2.1), то расстояние от т. О до фронта равно nr, и решения (2.2) можно представить в следующей форме:

, (2.7)

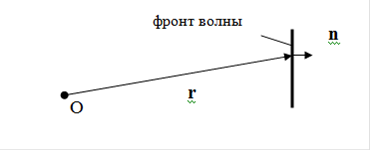
Рис. 2.1. Перемещающийся фронт радиоволны

Справедливость (2.7) нетрудно проверить подстановкой в уравнения (2.2).

Выражения (2.7) описывают монохроматическую волну, т. е. волну, векторы напряженности которой меняются во времени по гармоническому закону с одной определенной частотой.

Найдем скорость распространения радиоволны как скорость перемещения ее фронта (рис.2.1). На такой поверхности фаза y = wt - kr = wt - knr = Const, следовательно,

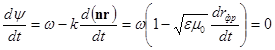(2.8)

здесь rфр - проекция r на направление перемещения фронта волны.

Из (2.8) следует, что

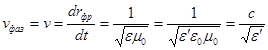где .

Определим ориентацию векторов E и H волны относительно направления распространения и между собой. Векторные операции в (2.1) можно выразить с помощью оператора :

divE = ÑE, rotE = [Ñ, E], divH = ÑH, rotH = [Ñ, H].

Применим Ñ к экспоненте в (2.7). Поскольку kr = kxx + kyy + kyz, то Ñei(wt - kr) = =eiwt Ñe -ikr = eiwt(-ik)e -ikr = -ik ei(wt - kr). Тогда два последних уравнения системы (2.1) можно записать как

divE = ÑE = -i(kE) = 0, divH = ÑH = -i(kH) = 0. (2.9)

Из (2.9) следует, что векторы E и H перпендикулярны волновому вектору k, а, следовательно, и направлению распространения волны.

Проанализируем теперь второе уравнение системы (2.1).

Перейти на страницу: 1 2

Самое читаемое:

Анализ линейной активной цепи
В данной курсовой работе необходимо выполнить анализ линейной активной цепи. Целью проектирования является закрепление навыков и умений студентов в области построения и анализа частотных, временных, спектральных характеристик радиотехнических цепей, нахождение формы сигнала на выходе цепи, исследование влияния параметров цепи на хар ...