Разделы сайта
- Главная
- Исследования и анализ современных технологий
- IP-телефония
- Антенно-фидерные устройства
- Виртуальное построение рабочей локальной сети
- Влияние электромагнитного поля на подземную проволочную антенну
- Микрополосковая антенная решетка
- Система экологического мониторинга вредных газовых выбросов
- Организация процесса производства цифрового телевиденья
Построение переходного процесса САР Смита
Для того чтобы построить переходный процесс построим дискретные модели.
1) y(i)=
* y( i-1) + 
(U ( i-
) + W (i-
) )
Где i=0,1…800
В качестве регулирующего блока рассмотрим ПИ - регулятор:
2) U(i) = 
(i) + 
(i); 
(i) = 
;
; 
; 
) 
(i) = ε(i) - 
; ε(i) = 
;
) 
;
) 
Моделируем САР при условии, что наша модель адекватна реальному объекту.
Рассчитываем все вышеперечисленные параметры. По полученным данным строим переходный процесс САР Смита при условии i=0,1…800.
График переходного процесса САР Смита представлен на рисунке.
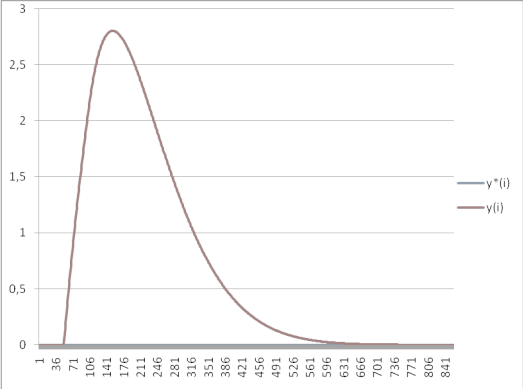
Рисунок: График переходного процесса САР Смита
Исследование устойчивости САР Смита
По полученному графику перехолного процесса можно судить о его сути, качестве регулирования аналогично тому что было сделано ранее.
В данном случае из графика мы видим, что процесс получился апериодический, максимальное динамическое отклонение равно 2,86 и время регулирования равно 617 секундам.
Самое читаемое:
Инерционное звено первого порядка
инерционное звено автоматическое
регулирование
Современное
производство характеризуется непрерывным увеличением производительности
агрегатов, повышением качества выпускаемой продукции и снижением ее стоимости.
Большие скорости протекания производственных процессов и повышение требований к
точности их выдерживания привели к широкому ...