Разделы сайта

Выделение огибающей узкополосного случайного процесса. Квадратурный демодулятор

Удобным инструментом для анализа узкополосных сигналов является комплексная огибающая сигнала [6].

В общем случае (в зависимости от вида модуляции) у сигнала s (t) может изменяться как амплитуда, так и начальная фаза:

(t) = A (t) ∙cos (ω0∙t +φ (t)) (54)

(t) - амплитудная огибающая (закон, по которому изменяется амплитуда); φ (t) - фазовая функция закон (закон, по которому изменяется начальная фаза). Весь аргумент функции cos называется полной фазой сигнала ψ (t) = ω0∙t + φ (t), тогда https://safe-str.ru/brands/safetronics-slovakiya/ Сейф взломостойкий Safetronics.

(t) = A (t) ∙cos (ψ (t)) (55)

Сигнал (1) можно представить как вещественную часть комплексной функции, заменив косинус комплексной экспонентой.

(t) =Re (A (t) ·exp (j·ψ (t))) (56)

По формуле Эйлера

(j·ψ (t))) = cos (ψ (t)) + j· sin (ψ (t)), следовательно Re (exp (j·ψ (t))) = cos (ψ (t)).

Проанализируем функцию A (t) ·exp (ψ (t)).

(t) ·exp (j·ψ (t)) = A (t) ·exp (j· (ω0∙t +φ (t))) = A (t) ·exp (j·ω0∙t) · exp (j·φ (t)) (57)

Множитель exp (j·ω0∙t) представляет собой немодулированное несущее колебание и является быстроменяющимся, а A (t) ·exp (j·φ (t)) меняется, как правило, значительно медленнее и содержит информацию об амплитудной огибающей и начальной фазе одновременно. Этот медленноменяющийся множитель и называется комплексной огибающей сигнала:

(58)

Комплексная огибающая содержит всю необходимую информацию для декодирования сигнала и вычисления его мощностных и фазовых характеристик.

Представим комплексную огибающую в косинусно-синусной форме, воспользовавшись формулой Эйлера, тогда:

=A (t) ·cos (φ (t)) + A (t) ·j·sin (φ (t)) =i (t) + j∙q (t) (59)

(t) =A (t) ·cos (φ (t)) - синфазная (косинусная) компонента комплексной огибающей; q (t) =A (t) ·sin (φ (t)) - квадратурная (синусная) компонента комплексной огибающей.

Тогда A (t) ·exp (j·ψ (t)) можно представить в виде

(t) ·exp (j·ψ (t)) = (i (t) +j∙q (t)) ·exp (j·ω0∙t) =

= (i (t) +j∙q (t)) ∙ (cos (ω0∙t) + j∙sin (ω0∙t)) =

=i (t) ∙ cos (ω0∙t) +i (t) ∙j∙sin (ω0∙t) + j∙q (t) ∙cos (ω0∙t) + j∙q (t) ∙j∙sin (ω0∙t) =

=i (t) ∙ cos (ω0∙t) - q (t) ∙ sin (ω0∙t) +j∙ (i (t) ∙sin (ω0∙t) +q (t) ∙cos (ω0∙t)) (60)

s (t) = i (t) ∙cos (ω0∙t) - q (t) ∙sin (ω0∙t) (61)

На основе формулы (61)

можно построить векторный модулятор, с помощью которого можно получить любые виды модуляции. При этом амплитудная огибающая A (t) =, фазовая функция φ (t) =arctan (q (t) /i (t)) На рисунке 4 представлена функциональная схема векторного модулятора.

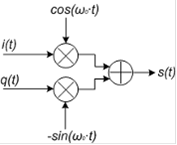
Рисунок 4 - Функциональная схема векторного модулятора

Так как cos (ω0∙t + π/2) =-sin (ω0∙t), то формулу можно переписать в виде s (t) = i (t) ∙cos (ω0∙t) +q (t) ∙cos (ω0∙t +π/2). Таким образом, в схему на рисунке 5 нужно ввести фазовращатель на угол π/2.

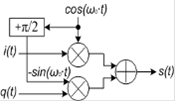
Рисунок 5 - Функциональная схема векторного модулятора с фазовращателем

Для выделения из сигнала комплексной огибающей используется процедура гетеродинирования. Входной ВЧ-сигнал s (t) = A (t) ∙cos (ω0∙t +φ (t)) умножается на колебание двух генераторов (гетеродинов) с частотой ω0, сдвинутых по фазе друг относительно друга на угол π/2 cos (ω0∙t) и - sin (ω0∙t).

(t) ∙cos (ω0∙t) = A (t) ∙cos (ω0∙t +φ (t)) ∙cos (ω0∙t) =

,5∙ A (t) ∙cos (φ (t)) + 0,5∙ A (t) ∙cos (2ω0∙t +φ (t)) = (62)

Перейти на страницу: 1 2

Самое читаемое:

Модернизация микрокриогенной системы
Микрокриогенная система (МКС) - автономная электроустановка, работающая по принципу низкотемпературного теплового насоса, и являющаяся важной составной частью радиотелескопов интерферометрического комплекса "Квазар-КВО" [1]. Радиоинтерферометрический комплекс "Квазар-КВО" - специализированный комплекс для реше ...