Разделы сайта

Моделирование помехи

Для осуществления моделирования необходимо создать шумовую выборку, плотность распределения вероятности которой подчинялась бы выражению (1). В качестве константы в выражении (1) выступает величина , полученная путем использования свойства плотности распределения:

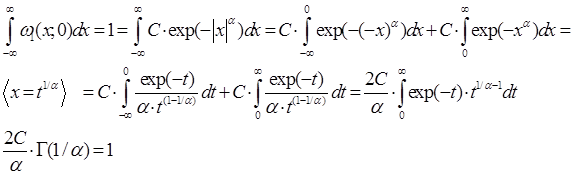
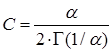. (75)

В итоге окончательное выражение для плотности распределения помехи примет вид:

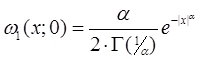, [1; 4]. (76)

Исходя из полученного выражения, получается интегральная функция распределения величины x:

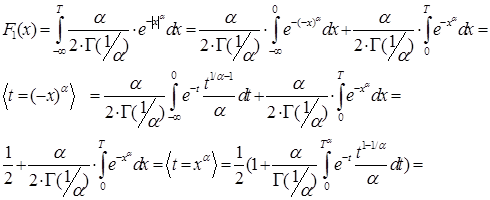
, (77)

где - неполная гамма-функция.

Далее, исходя из свойства о том, что если случайную величину , распределенную равномерно на интервале (0, 1), подвергнуть преобразованию по закону , то восстанавливается реализация случайной величины, распределенной по закону (77) с плотностью распределения 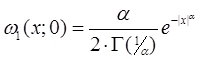. Именно таким образом моделируется шумовая выборка для различных значений параметра α.

Следует заметить, что дисперсия указанной помехи равна 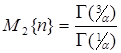. Для того, чтоб сравнивать эффективность работы алгоритмов при воздействии различных помех, эти помехи должны иметь одинаковые дисперсии. Поэтому случайную величину необходимо умножать на коэффициент, равный 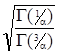. Данная нормировка позволяет получить дисперсию:

. (78)

Самое читаемое:

Инерционное звено первого порядка
инерционное звено автоматическое регулирование Современное производство характеризуется непрерывным увеличением производительности агрегатов, повышением качества выпускаемой продукции и снижением ее стоимости. Большие скорости протекания производственных процессов и повышение требований к точности их выдерживания привели к широкому ...