Разделы сайта

Расчёт допусков влияния разброса параметров на характеристики МПИ

микрополосковый антенна сопротивление частота

Изменение геометрических параметров излучателя и отклонения диэлектрической проницаемости материала и толщины подложки вызывают расхождения между расчетными и истинными значениями параметров МПИ.

Это в основном относится к резонансной частоте.

Поскольку полоса рабочих частот МПИ составляет обычно несколько процентов от средней частоты, то определение истинного значения резонансной частоты является весьма важным при проектировании МПИ и, соответственно микрополосковых антенн.

Точность изготовления пластины МПИ определяется способом производства и при использовании современных технологических методов может быть весьма высокой. Листовые диэлектрические материалы промышленного производства на базе полиэтилена и полистирола имеют допуски на относительную диэлектрическую проницаемость ±1% и ±5% на толщину.

Резонансная частота МПИ определяется следующей формулой:

где:

с - скорость света в вакууме.= 17.03ГГц.

На основе выражения для резонансной частоты получена следующая расчетная формула для относительной девиации частоты:

Так как , то членом 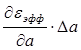можно пренебречь.

Частные производные, входящие в формулу для относительной девиации частоты определяются по формулам:

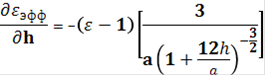
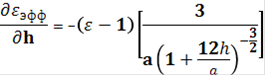где Δh = 0,05·h = 0.00002193 - 5%-ый допуск на толщину листового диэлектрического материала, заложенный при производстве;

Δε = 0,25 - допуск на значение относительной диэлектрической проницаемости.

В результате вычислений, значение относительной девиации частоты получилось таким:

Самое читаемое:

Метод частотной модуляции радиотехнического сигнала
За последнее время существенно повысился технический уровень электронной техники. Быстрое развитие требует создания все более точного и сложного автоматизированного технологического оборудования для изобретения более сложных и совершенных устройств с лучшими характеристиками и параметрами, меньшими габаритами. Для у ...