Разделы сайта

Подпрограмма статистической обработки

Обработка результатов наблюдений при прямых измерениях.

Измерения не могут быть выполнены абсолютно точно. Всегда имеется некоторая неопределенность в значении измеряемой величины. Нашей задачей является найти оценку отклонения истинной величины от измеренной. Погрешности физических измерений принято подразделять на систематические, случайные и грубые. Нас же интересуют случайные, проявление которых неодинаково в каждом измерении и не может быть учтена. Закономерности, описывающие поведение случайных величин, изучаются теорией вероятностей.[17].

При статистической обработке результатов наблюдений выполняются следующие операции:

1) Находим среднее арифметическое всех n измерений xi , где i принимает значения от 1 до n:

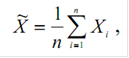
где n ⎯ число результатов наблюдений; Xi ⎯ i-ый результат наблюдения.

2) Оцениваем дисперсию (среднеквадратичная погрешность - отклонение от среднего - СКО)

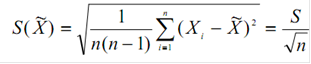
3) Находим случайную абсолютную погрешность прямого измерения:

где t(n,p) - коэффициент Стьюдента, который зависит от числа измерений n и вероятности p, с которой мы хотим указать погрешность ∆xсл( половина доверительного интервала для среднего арифметического). Полученные значения сравниваются с погрешностью градуировки прибора и, если они различаются на порядок и более, то берется наибольшее из них. Если они сравнимы по величине, то полную погрешность вычисляют как корень квадратный из суммы квадратов этих погрешностей.[18].[9].

4) Находим относительную погрешность прямого измерения:

5) Выводим результат в виде:

Программа приведена в приложении Д.

Самое читаемое:

Вакуумные и плазменные приборы
Спроектировать электронно-оптическую систему осциллографической трубки. Исходные данные к проекту: . Ускоряющее напряжение - 5 кВ. . Ток эмиссии катода - 1 мА. . Диаметр луча на экране - 0,5 мм. . Развертка луча - линейная. . Угол отклонения луча - 200. Напряжение, В 6.3 ...