Разделы сайта

Выбор критериев качества

Поскольку функцию можно считать непрерывной и заданной на конечном отрезке, то ее можно с любой заданной точностью аппроксимировать полиномом степени . В таком случае она принимает вид

, (3.4)

где , - вещественные коэффициенты.

Воспользовавшись выражениями (3.2) и (3.4) критерий представим в виде:

. (3.5)

Поскольку

то с учетом (3.5) получим неравенство

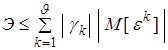. (3.6)

Следовательно, выполнению требования (3.3) способствует выполнение условий

. (3.7)

Таким образом, вместо одного универсального, но неконтролируемого критерия , получено множество критериев, значения которых можно определить, если имеется достоверная информация о функции распределения случайного процесса .

, , (3.8)

Чтобы получить такую информацию необходимо определить статистические характеристики всех возмущающих воздействий и располагать достаточно точной математической моделью управляемого объекта.

На основании условий (3.7) приходим к выводу, что задача оптимального управления технологическими процессами должна ставиться и решаться как задача многокритериальной оптимизации, т.к. в условиях оптимальности управления (3.7) используется не один, а несколько критериев (3.8).

Однако, выполнить условия (3.7) на практике оказывается весьма затруднительным, хотя бы по причине требуемого для этого объема информации о статистических характеристиках ошибки управления . Поэтому необходимо определить критерии, которые было бы проще контролировать в процессе управления, чем статистические моменты величины .

Доказано, что при управлении непрерывными стационарными системами в условиях статистической неопределенности критерии (3.8) одновременно приближаются к своим минимальным значениям, если обеспечено выполнение требования

, (3.9)

где - свободный член характеристического уравнения замкнутой системы.

Это уравнение можно представить в виде

, (3.10)

где - комплексная переменная; -целое положительное число (порядок характеристического уравнения); , - постоянные вещественные коэффициенты; , - корни характеристического уравнения; - характеристический полином (функция) замкнутой системы.

Чтобы обеспечить необходимый запас устойчивости используют следующие ограничения на расположение корней характеристического уравнения (3.10):

; (3.11)

Перейти на страницу: 1 2 3 4

Самое читаемое:

Мощный импульсный стабилизированный блок питания
Процесс в развитии науки и техники не стоит на месте. Большую роль в этом процессе играет технология, так как от правильно выбранной или разработанной технологии зависят и характеристики конкретного изделия и его стоимость. Необходимость проектирования сложных радиоэлектронных средств (РЭС) и требования к сокращению сроков их про ...