Разделы сайта

Теория расчета узкополосных фильтров с минимальными потерями в середине полосы пропускания и заданным затуханием в полосе запирания

В различных практических случаях требуются узкополосные фильтры с возможно меньшими потерями в середине полосы пропускания и заданным высоким затуханием на некоторой частоте полосы запирания. Обычно в диапазоне СВЧ ширина полосы сигнала мала по сравнению с несущими частотами. Примерный вид зависимости потерь от частоты полосового узкополосного фильтра можно увидеть на рис. 4.4.

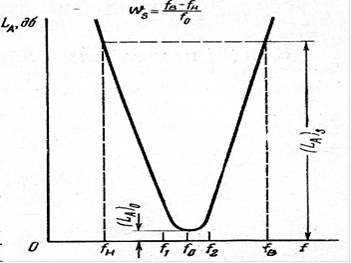
Рис. 4.4«Зависимость затухания от частоты»

Рассматриваемые фильтры обладают достаточно узкой полосой пропускания, поэтому вне зависимости от структуры применяемых резонаторов и связей будет справедливо упрощенное частотное преобразование:

, (4.1)

где

(4.2)

, (4.3)

где f0 - центральная (средняя) частота, f2 - верхняя частота полосы пропускания, f1- нижняя частоты полосы пропускания.

S= (4.4)

Все входящие в формулы (4.1) - (4.4) изображены на рисунке см. рис. 4.4.

В формуле (4.1) величина представляет собой относительную ширину полосы пропускания, соответствующую полосе прототипа с граничной частотой ω1’.Значение имеет также относительная ширина полосы S, в пределах которой затухание должно достигнуть заданного высокого уровня (LA)S (см. рис. 4.4). Затухание (LA)0 в середине полосы должно быть сведено к минимуму.

Многие расчеты, основывающиеся на прототипах нижних частот, приводят к таким конструкциям полосно-пропускающих фильтров, у которых затухание (LA)0 равно нулю, если нет потерь в резонаторах фильтра. Но когда в расчете учтены неизбежные потери в резонаторах, затухание (LA)0 всегда будет не равно нулю. При этих условиях фильтры с одинаковыми величинами S для заданного затухания могут иметь значительно отличающиеся друг от друга затухания в середине полосы (LA)0 .

После длительных исследований было найдено для общего случая произвольного числа резонаторов, что малую величину (LA)0 можно получить, если фильтр рассчитать из прототипа нижних частот (см. рис. 4.2) со следующими параметрами:

g0= g1= g2=…= gn= gn+1=1 (4.5 а)

ω1’=1 (4.5 б)

Следует отметить, что эти обозначения имеют следующий смысл:

gk, где k=1…n - индуктивность последовательной катушки или емкость параллельного конденсатора;

g0 - сопротивление генератора R’0, если g1= C’1, или проводимость генератора G’0 , если g1= L’1;

gn+1 - сопротивление нагрузки R’n+1, если gn= C’n, или проводимость нагрузки G’n+1, если gn= L’n.

Приведем несколько уравнений, помогающихпонять, как рассчитывать фильтры.

Выражение для оценки влияния потерь рассеяния в прототипах нижних частот при =0:

, дБ, (4.6)

где dk= 1 /Qk ,

dk - параметр, именуемый, как коэффициент рассеяния,

Qk - добротности k-ых элементов, под которыми будем понимать добротности элементов фильтров нижних частот на частоте среза 1, определяемые выражениями:

Qk=1 * Lk/ Rk или Qk=1 * Сk/ Gk ,

где Rk - паразитное сопротивление катушки (индуктивности Lk);

Перейти на страницу: 1 2

Самое читаемое:

Анализ и синтез систем автоматического регулирования
Цель настоящей работы - выбор и обоснование типов регуляторов положения, скорости и тока, а также расчет параметров настройки этих регуляторов. Для синтеза автоматической системы будем использовать метод поконтурной оптимизации с использованием методов модального и симметричного оптимума. При функциональном проектировании автомат ...