Разделы сайта

Непрерывный и квантованный объекты управления в пространстве состояний

1. Задана линейная стационарная дискретная система (параметры непрерывных динамических звеньев в таблице 1 Приложения 2).

и .

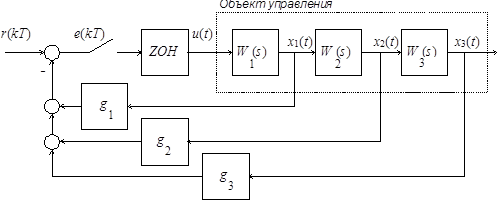
Рисунок 1. Структурная схема линейной стационарной дискретной системы

. Составить описание непрерывного объекта управления в пространстве состояний.

. Выбрать период дискретности и обосновать его выбор.

. Получить описание квантованного объекта управления в пространстве состояний.

. Определить параметры матрицы обратной связи G

, располагающей собственные значения замкнутой системы точках =0.9, =, = (таблица 2 Приложения 2). Для расчета коэффициентов обратной связи использовать метод канонической формы фазовой переменной. Для синтезированной системы построить ее корни на комплексной z-плоскости и график переходного процесса при единичном ступенчатом воздействии.

. При выбранных параметрах матрицы обратной связи G

определить установившуюся ошибку при подаче на вход системы сигнала 1,32*1(t) (таблице 3 Приложения 2).

. Получить дискретную передаточную функцию замкнутой системы управления по каналу, r(z) -> x3(z) (таблице 4 Приложения 2). По полученной передаточной функции составить разностное уравнение.

. Составить блок-схему алгоритма или написать программу на любом языке программирования высокого уровня, реализующую дискретную передаточную функцию замкнутой системы управления на основе полученного разностного уравнения (по п.1.7).

Самое читаемое:

Анализ линейной активной цепи
В данной курсовой работе необходимо выполнить анализ линейной активной цепи. Целью проектирования является закрепление навыков и умений студентов в области построения и анализа частотных, временных, спектральных характеристик радиотехнических цепей, нахождение формы сигнала на выходе цепи, исследование влияния параметров цепи на хар ...