Разделы сайта

• Главная
• Исследования и анализ современных технологий
• IP-телефония
• Антенно-фидерные устройства
• Виртуальное построение рабочей локальной сети
• Влияние электромагнитного поля на подземную проволочную антенну
• Микрополосковая антенная решетка
• Система экологического мониторинга вредных газовых выбросов
• Организация процесса производства цифрового телевиденья

Геометрическая иллюстрация

На отрезке длиной 2h строится парабола (рис.1.4), проходящая через три точки ,. Площадь под параболой, заключенная между осью OX и прямыми, принимают равной интегралу.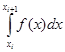

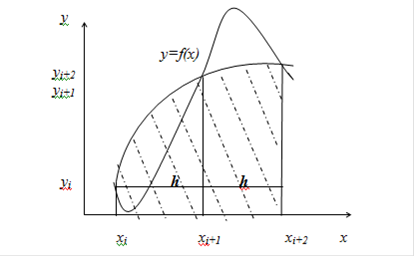
Рис.1.4. Геометрическая иллюстрация метода парабол

Особенностью применения формулы Симпсона является тот факт, что число разбиений отрезка интегрирования - четное.

Если же количество отрезков разбиения - нечетное, то для первых трех отрезков следует применить формулу, использующую параболу третьей степени, проходящую через четыре первые точки, для аппроксимации подынтегральной функции.

(1.3)

Это формула Симпсона «трех восьмых».

Для произвольного отрезка интегрирования формула (1.3) может быть «продолжена»; при этом число частичных отрезков должно быть кратно трем ( точек).

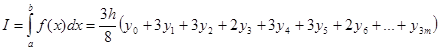
, m=2,3, .

- целая часть

Алгоритм оценки погрешности формулы Симпсона можно записать в виде:

где - коэффициент, зависящий от метода интегрирования и свойств подынтегральной функции; - шаг интегрирования;- порядок метода.

Правило Рунге применяют для вычисления погрешности путем двойного просчета интеграла с шагами h и kh.

(1.5)

(1.5) - апостериорная оценка. Тогда Iуточн.= +Ro, уточненное значение интеграла .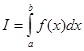

Если порядок метода неизвестен, необходимо вычислить I в третий раз с шагом , то есть:

из системы трех уравнений:

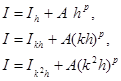
с неизвестными I, А и p получаем :

(1.6)

Из (1.6) следует

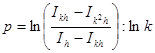
Таким образом, метод двойного просчета, использованный необходимое число раз, позволяет вычислить интеграл с заданной степенью точности. Выбор необходимого числа разбиений осуществляется автоматически. Можно при этом использовать многократное обращение к подпрограммам соответствующих методов интегрирования, не изменяя алгоритмов этих методов.

Самое читаемое:

Контроллер опорно-поворотного устройства антенны
Микроконтроллеры уверенно и, по-видимому, навсегда завоевали место в нашей жизни. Найти хоть одно электронное изделие, не имеющее микроконтроллеров, практически невозможно. Разнообразные элементы схем в видеомагнитофонах, DVD - плеерах, телевизорах и микроволновых печах, автоматических дверях, системах управления лифтами, промышлен ...