Разделы сайта

Выбор шага интегрирования

Для выбора шага интегрирования можно воспользоваться выражением остаточного члена. Возьмем, например, остаточный член формулы Симпсона:

Если ê ê, то ê ê.

По заданной точности e метода интегрирования из последнего неравенства определяем подходящий шаг.

, .

Однако такой способ требует оценки (что на практике не всегда возможно). Поэтому пользуются другими приемами определения оценки точности, которые по ходу вычислений позволяют выбрать нужный шаг h.

Один из таких приемов.

Пусть 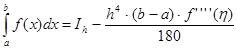, где - приближенное значение интеграла с шагом . Уменьшим шаг в два раза, разбив отрезок на две равные части и ().

Тогда ,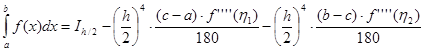

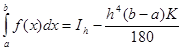Предположим теперь, что меняется не слишком быстро, так что почти постоянна: . Тогда и 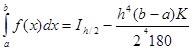, откуда , то есть .

Отсюда можно сделать такой вывод: если , то есть если , , а - требуемая точность, то шаг подходит для вычисления интеграла с достаточной точностью. Если же , то расчет повторяют с шагом и затем сравнивают и и т.д. Это правило называется правилом Рунге.

Однако при применении правила Рунге необходимо учитывать величину погрешности вычислений: с уменьшением абсолютная погрешность вычислений интеграла увеличивается (зависимость от обратно пропорциональная) и при достаточно малых может оказаться больше погрешности метода. Если превышает , то для данного шага применять правило Рунге нельзя и желаемая точность не может быть достигнута. В таких случаях необходимо увеличивать значение .

Перейти на страницу: 1 2

Самое читаемое:

Использование микроконтроллера в системах управления
В современных системах управления микропроцессорная техника все чаще и чаще находит себе место. Это объясняется простотой ее внедрения, использования и модификации. Микроконтроллеры представляют собой приборы, конструктивно выполненные в виде одной БИС и включающие в себя все устройства необходимые для реализации цифро ...