Разделы сайта

Принцип Гюйгенса и зоны Френеля

Зоны Френеля могут быть построены на поверхности произвольной формы. Найдём радиус n-й зоны Френеля на плоскости S, перпендикулярной направлению распространения, в предположении, что распространяется плоская радиоволна. Согласно обозначениям рис. 2.6.

Рис. 2.6. К определению радиусов зон Френеля

(2.19)

Если выполняется условие l1, l2 >> l, то

, (2.20)

Подставив выражения (2.20) в (2.19), нетрудно получить

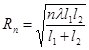
Зафиксируем на плоскости S, перпендикулярной трассе AB, точки образующей n-й зоны Френеля и будем перемещать S вдоль трассы (рис. 2.6). Из (2.19) следует, что в этом случае выполняется равенство

(2.21)

Математически (2.21) есть уравнение эллипса, следовательно, границы зон Френеля в пространстве представляют собой поверхности эллипсоидов вращения с фокусами в точках А и В. Области пространства между двумя соседними эллипсоидами называют пространственными зонами Френеля. Максимума радиус сечения эллипсоида плоскостью S достигает при l1 = l2 = AB/2:

Рис. 2.7. Построение границ пространственных зон Френеля

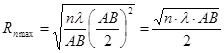
Экспериментально существование зон Френеля подтверждается, например, изменчивостью в точке приёма B напряжённости поля, создаваемого источником в т. A, при изменении радиуса R отверстия в условно бесконечном экране (рис. 2.8.). В полном соответствии с принципом Гюйгенса сложение сигналов от неперекрытых еще зон Френеля приводит к колебаниям сигнала.

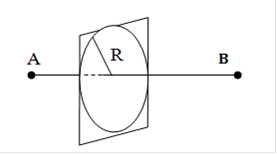
Рис. 2.8. Пропускание радиоволны через отверстие в экране

Перейти на страницу: 1 2

Самое читаемое:

Изготовление цифрового прибора для контроля осанки и зрения при работе на персональном компьютере
Современную жизнь невозможно представить без электроники и ее важнейшей отрасли - микроэлектроники. В любом месте - на работе и в быту - изделия из электроники окружают человека. Она трудится повсюду - в сверхглубоких скважинах и в подводных аппаратах - батискафах, в самолетах и космических кораблях, на атомных электростанциях и рад ...