Разделы сайта

Представление сигнала и спектр

Есть два способа представления сигнала в зависимости от области определения: временной и частотный. В первом случае сигнал представляется функцией времени характеризующей изменение его параметра.

Кроме привычного временного представления сигналов и функций при анализе и обработке данных широко используется описание сигналов функциями частоты. Действительно, любой сколь угодно сложный по своей форме сигнал можно представить в виде суммы более простых сигналов, и, в частности, в виде суммы простейших гармонических колебаний, совокупность которых называется частотным спектром сигнала.

Для перехода к частотному способу представления используется преобразование Фурье:

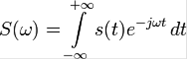
Функция называется спектральной функцией или спектральной плотностью.

Поскольку спектральная функция является комплексной, то можно говорить о спектре амплитуд и спектре фаз . Физический смысл спектральной функции: сигнал представляется в виде суммы бесконечного ряда гармонических составляющих (синусоид) с амплитудами , непрерывно заполняющими интервал частот от 0 до и начальными фазами .

Размерность спектральной функции есть размерность сигнала, умноженная на время.

Самое читаемое:

Исследование зон затенения сигналов систем сотовой связи в районах г. Йошкар-Олы
С начала 70-х годов внимание исследователей и инженеров во многих странах было обращено к проблеме распространения ультракоротких волн (УКВ) в городах. Это связано с интенсивным развитием систем радиосвязи различного назначения - от телевидения до систем связи с подвижными объектами и радиотелефонии, играющих в жизни городов ...